Problemi per la lezione del 21/01
- [Metodo arePipppere] Due curve C e C' sono dette pipppere se e solo se esiste un x intero
compreso fra 1 e 10 tale che i punti (x,x) e (2*x,2*x) appartengono a entrambe le curve e il punto (x+1,1.5*x*x) appartiene ad almeno
una delle due curve.
Aggiungete alla classe Curva un metodo statico boolean arePipppere(Curva c1, Curva c2) che date due curve restituisce true sse le curve sono pipppere. Verificate, usando questo metodo che la retta y=x e la parabola y=-3x^2+19x-24 sono pipppere.
- [Classe Iperbole] Definite una classe Iperbole che estende Curva e le cui istanze rappresentano iperboli i cui semiassi giacciono sugli assi cartesiani. Decidete voi di quali costruttori e metodi dotarla.
- [Pacchetto my.geom] Spostate tutte le classi della gerarchia geometrica realizzata in queste ultime lezioni in un pacchetto di nome my.geom, e realizzate una classe Test (nel pacchetto senza nome) che importi e utilizzi alcune della classi e metodi del pacchetto appena creato.
- [Curva di Koch (1)] Per questo problema, rispolverate la libreria per la turtlegraphics. Scrivete una classe
Koch che nel costruttore istanzi un campo e una tartaruga e che abbia un metodo disegna(int x) che si limita a disegnare un segmento di lunghezza
data. Scrivete una classe con un metodo main che istanzi la classe Koch e che poi disegni un segmento di lunghezza 10. Quando siete certi che
funzioni, modificate il metodo disegna in modo che invece di disegnare un segmento, disegni una curva come quella chiamata F1 nella figura.
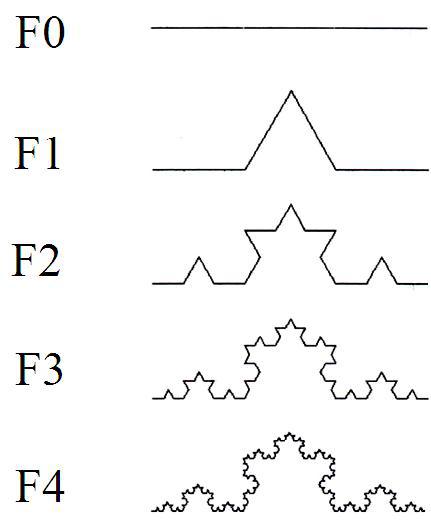
- [Curva di Koch (2)] Ora modificate la classe trasformando il metodo disegna in uno di segnatura disegna(int liv,int x) che, se liv==0 disegna un segmento di lunghezza x, altrimenti muove la tartaruga come nella figura F1 ma, ogni volta che la tartaruga dovrebbe disegnare un segmento, invochi invece disegna(liv-1,x).
- [Fiocco di neve] Disegnate tre curve di Koch su un triangolo equilatero, ottenendo un fiocco di neve:

- [Doppia curva di Koch] Disegnate una curva chiamata DKoch (doppia curva di Koch) ottenuta in un modo simile al disegno di base di Koch, ma modificato
nel seguente modo:
- la tartaruga procede disegnando la curva a quattro segmenti del tracciato di Koch originale;
- dopo aver girato su se stessa di 180 gradi, la tartaruga ripete il disegno esattamente nello stesso modo (ovviamente il triangolo risulterą speculare al precedente, formando con esso una sorta di rombo);
- dopo aver girato di nuovo su se stessa di 180 gradi, la tartaruga ripete il disegno per la terza ed ultima volta: stavolta di fatto ricalcherą il disegno fatto nella prima fase.
